Uncovering New Perspectives on Perfect Numbers: Beyond Euclid and Euler

📅 Published on November 5, 2024

Perfect numbers, positive integers equal to the sum of their proper divisors, have intrigued mathematicians for centuries. Traditionally, efforts to identify perfect numbers have focused on finding Mersenne primes, as established by the Euclid-Euler theorem, which characterizes all known even perfect numbers , as explored in the previous article. However, the existence of odd perfect numbers remains one of the great unsolved mysteries in mathematics, with no examples discovered to date.

This article introduces a novel algorithm that shifts focus from Mersenne primes to “beautiful triangular numbers,” a broader class that could potentially include odd perfect numbers, a hypothesis that will be further justified in the following section. By leveraging advanced mathematical libraries, efficient factorization, and computational optimizations, this approach aims to explore new ground in the search for perfect numbers, extending beyond the constraints of the Euclid-Euler framework.

Through this exploration, we seek to open fresh perspectives on perfect numbers, blending theory with computation to push the boundaries of number theory.

I. Proper Definition of a Triangular Number

A triangular number is a figurate number that can be represented as a triangle with dots. It is the sum of the first \( n \) natural numbers, and the \( n \)-th triangular number \( T_n \) is given by the formula:

$$ T_n = \frac{n(n + 1)}{2} $$

For example:

• The 1^st triangular number is \( T_1 = 1 \).
• The 2^nd triangular number is \( T_2 = 1 + 2 = 3 \).
• The 3^rd triangular number is \( T_3 = 1 + 2 + 3 = 6 \).
• The 4^th triangular number is \( T_4 = 1 + 2 + 3 + 4 = 10 \), and so on.

II. Why Triangular Numbers?

The choice to focus on triangular numbers stems from their inherent sequential and structural properties, which offer a broader framework for exploring perfect numbers and prime relationships beyond the Euclid-Euler theorem. Here’s a detailed rationale:

1. Sequential Nature of Triangular Numbers

Triangular numbers are generated by the sequential addition of natural numbers, ensuring that every integer contributes to the sequence. Mathematically, the \( n \)-th triangular number is expressed as:

$$ T_n = \frac{n(n + 1)}{2} $$

This formula guarantees that for each \( n \), the corresponding triangular number \( T_n \) is uniquely determined without relying solely on the properties of Mersenne primes. Consequently, the triangular number sequence encompasses both even and odd values, as well as prime and composite numbers. This comprehensive inclusion provides a complete and uninterrupted structure, offering potential avenues for discovering patterns or properties applicable to perfect numbers and primes beyond the established Euclid-Euler framework.

2. Inclusion of Odd Triangular Numbers

The sequence of triangular numbers naturally includes a diverse array of numbers, including those that are neither perfect nor primes. For instance, numbers such as 15 (\( T_5 \)), 21 (\( T_6 \)), and 45 (\( T_9 \)) are triangular but do not correspond to perfect numbers. This diversity allows for the identification and analysis of various mathematical patterns and relationships, which may, in turn, inform the search for perfect numbers or new prime structures that are not captured by the Euclid-Euler theorem.

3. Validation of the Theory

To validate this theory, it is necessary to identify all the divisors of triangular numbers within a specific arrangement that fits this structure. Alternatively, a new structure must be discovered where all the divisors are accounted for in a systematic and coherent manner. This ensures that the theory aligns with both the known properties of triangular numbers and the broader framework of number theory, paving the way for deeper insights into perfect numbers and their relationships with primes.

The reasoning behind this idea is that if a perfect number has a specific geometric form, such as a triangular or polygonal shape, its divisors should naturally exhibit a complementary structure within this form. This means that divisors of the perfect number would not be randomly distributed but would follow a systematic arrangement or pattern within the geometry of the number itself. By exploring these patterns, especially for triangular numbers, we can identify whether the divisors align in a consistent way that corresponds to both the structural properties of the number and the relationships that underpin perfect numbers and their divisors. This alignment could, therefore, reveal deeper links between perfect numbers, primes, and geometric representations, offering a new framework for understanding number theory through these patterns.

4. Beautiful Triangular Numbers and Their Relation to Primes

Among triangular numbers, those that are also perfect numbers exhibit a particular relationship with prime numbers. Specifically, all even perfect numbers are triangular numbers of the form:

$$ N = 2^{p-1}(2^p – 1) = \frac{(2^p – 1)(2^p)}{2} = T_{2^p – 1} $$

where \( p \) is a prime number and \( 2^p – 1 \) is a Mersenne prime. This observation aligns perfectly with the Euclid-Euler theorem, demonstrating that the side length of the triangular arrangement corresponds directly to the exponent in the Mersenne prime.

However, this characterization applies exclusively to even perfect numbers derived from Mersenne primes. The exploration of triangular numbers invites the consideration of other primes or number forms that could potentially lead to perfect numbers, thereby extending the search beyond Mersenne primes. Identifying such primes could unveil new perfect numbers or provide insights into the structure of primes, contributing to the ongoing quest to resolve the open problem of odd perfect numbers.

In this paper, the perfect triangular numbers are called beautiful triangular numbers.

5. Toward a New Framework for Perfect Numbers

The integration of triangular numbers into the study of perfect numbers offers a promising extension to the Euclid-Euler theorem. By leveraging the sequential and structural properties of triangular numbers, this approach broadens the scope of exploration beyond the confines of Mersenne primes, potentially unveiling new relationships and patterns that could lead to the discovery of additional perfect numbers or novel prime structures. This innovative methodology underscores the dynamic nature of number theory, where classical concepts are re-examined through fresh lenses to address longstanding mathematical challenges.

III. Proving Even Perfect Numbers are Triangular

Building upon the definitions and properties of perfect and triangular numbers, we now demonstrate that every even perfect number is indeed a triangular number. This connection not only reinforces the significance of the Euclid-Euler theorem but also broadens our understanding of the structural relationships between different classes of numbers.

1. Definitions

• Perfect Number: A positive integer \( n \) is called perfect if it is equal to the sum of its proper divisors (excluding itself). For example, \( 6 \) is perfect because its divisors \( 1, 2, \) and \( 3 \) sum to \( 6 \).
• Triangular Number: A number \( T_k \) is triangular if it can be expressed in the form:

$$ T_k = \frac{k(k + 1)}{2} $$

for some integer \( k \).

2. Even Perfect Numbers

According to the Euclid-Euler theorem, every even perfect number can be expressed in the form:

$$ P = 2^{p-1}(2^p – 1) $$

where \( 2^p – 1 \) is a prime number, known as a Mersenne prime.

3. Proving Even Perfect Numbers are Triangular

We aim to show that \( P = 2^{p-1}(2^p – 1) \) can be expressed as \( T_k = \frac{k(k + 1)}{2} \) for some integer \( k \).

a) Expressing the Perfect Number as a Triangular Number

Starting with the Euclid-Euler form:

$$ P = 2^{p-1}(2^p – 1) $$

Since \( T_k = \frac{k(k + 1)}{2} \), we set:

$$ T_k = P \quad \Rightarrow \quad \frac{k(k + 1)}{2} = 2^{p-1}(2^p – 1) $$

Multiplying both sides by 2:

$$ k(k + 1) = 2^p(2^p – 1) $$

b) Identifying the Relationship Between \( k \) and \( p \)

Observe that the right-hand side of the equation can be factored as:

$$ k(k + 1) = 2^p(2^p – 1) $$

Notice that:

• If we let \( k = 2^p – 1 \), then \( k + 1 = 2^p \).
• Substituting these into the equation:

$$ (2^p – 1)(2^p) = 2^p(2^p – 1) $$

This identity holds true, confirming that:

$$ k = 2^p – 1 $$

is a valid solution.

c) A Triangular Perspective on Euclid-Euler’s Theorem

Since \( k = 2^p – 1 \) satisfies the equation \( k(k + 1) = 2^p(2^p – 1) \), we have:

$$ P = T_k = \frac{k(k + 1)}{2} $$

Therefore, every even perfect number \( P \) can be expressed as a triangular number \( T_k \) where \( k = 2^p – 1 \). This establishes a direct correspondence between even perfect numbers and triangular numbers derived from Mersenne primes, highlighting the interconnectedness of these mathematical concepts.

IV. Beautiful Triangular Numbers

For millennia, certain numbers have been celebrated as perfect numbers due to their unique alignment between divisional and additive properties, specifically how their divisors sum to the number itself. While this traditional notion of “perfection” has deep historical roots, it might be seen as one interpretation among others rather than an absolute ideal. This article introduces an expanded concept: beautiful triangular numbers. Beautiful triangular numbers, like traditional perfect numbers, satisfy these divisional criteria but also reveal a broader aesthetic, where structural and divisional properties merge into a cohesive, harmonious framework. The term “beautiful” is used to highlight the balanced interplay within their divisors, forming a visual symmetry that could be represented as an elegant, symmetrical pattern illustrating their relationships. This perspective invites us to explore “perfection” through a lens of mathematical beauty, enriching our appreciation for the symmetry in these numbers.

1. Why “Beautiful” Triangular Numbers?

The designation of certain triangular numbers as “beautiful” stems from their adherence to specific mathematical properties that go beyond mere triangularity. These properties involve the relationships between their divisors and the way these divisors are organized and interact. The beauty lies in how these numbers respect both division and inclusion, creating a balanced and interconnected structure.

2. Properties of Beautiful Triangular Numbers

• Divisional Harmony: A beautiful triangular number T_k has a set of divisors that exhibit a balanced distribution. The divisors can be paired such that each pair multiplies to the triangular number itself, creating a symmetrical and harmonious structure.
• Interconnected Structure: The divisors of a beautiful triangular number follow a specific, interconnected pattern. Rather than being randomly distributed, the divisors maintain relationships that align with the number’s structure, forming an organized, cohesive arrangement.
• Structural Loop: When visualized, the relationships between the divisors of a beautiful triangular number create a loop-like structure. This loop represents the intricate balance between the number’s divisors, with each divisor contributing to the overall symmetry and balance of the number’s form.

3. Mathematical Justification

To identify a beautiful triangular number, we consider the following criteria:

1. Triangularity: The number must be a triangular number, satisfying:

$$ T_k = \frac{k(k + 1)}{2} $$

for some integer \( k \).

2. Divisor Pairing: The set of divisors \( D(T_k) \) of \( T_k \) can be paired such that each pair \( (d, \frac{T_k}{d}) \) satisfies a symmetrical relationship. This ensures that the divisors are evenly distributed around the central value of the number.
3. Inclusion Structure: The relationships between these divisor pairs exhibit inclusion properties akin to those in a Venn diagram. This means that for any two pairs \( (d_1, \frac{T_k}{d_1}) \) and \( (d_2, \frac{T_k}{d_2}) \), there exists a meaningful overlap or nesting that forms a cohesive loop, maintaining the structural integrity of the number’s divisor set.

4. Illustrative Example

Consider the triangular number \( T_6 = 21 \). Let’s examine its divisors and analyze its beauty based on the aforementioned properties:

• Divisors of 21: \( D(21) = \{1, 3, 7, 21\} \)
• Divisor Pairing:
  • \( (1, 21) \)
  • \( (3, 7) \)
• Inclusion Structure:
  • The pairs \( (1, 21) \) and \( (3, 7) \) demonstrate a clear hierarchical relationship where smaller divisors are nested within larger ones.
  • This nesting creates an overlapping structure that can be visualized as a loop, akin to interconnected circles in a Venn diagram.

This number fits the above criteria but is not a perfect number, so further examination is needed.

5. So, why beautiful?

Beautiful triangular numbers represent a captivating extension of traditional perfect numbers, expanding beyond the constraints of the Euclid-Euler theorem. While these numbers indeed satisfy the classical criteria of “perfection” through their unique divisional and additive properties, the framework underlying beautiful triangular numbers offers a broader, more nuanced approach. Rather than viewing perfection as a mere alignment of divisors and sums, beautiful triangular numbers emphasize a harmony of relationships, an elegant loop of division and inclusion that reveals hidden layers of symmetry. This approach invites us to see perfection not only as a definition but as an aesthetic quality, allowing us to explore the concept of “perfect” numbers through a lens that honors mathematical beauty. Beautiful triangular numbers, thus, may uncover new candidates for perfection, providing fresh insights and expanding our understanding of numerical symmetry.

V. Divisors in Beautiful Triangular Numbers

A perfect number is defined by the sum of its proper divisors. Therefore, to identify a prime without relying solely on the Euclid-Euler formula, it is essential to find the divisors within the triangular structure of the number.

To demonstrate a relationship between beautiful triangular numbers and their divisors, we seek a common property. Specifically, the diagonal of the triangle formed by a beautiful triangular number corresponds to a specific divisor, which we designate as the median divisor, known as “the power of two” in the context of the Euclid-Euler theorem. The median divisor is defined as the middle divisor in the sorted list of divisors, effectively acting as the median of the triangle.

1. Middle Divisor as the Triangle’s Median

The median divisor serves as the median of the triangle, ensuring a balanced distribution of divisors on either side. This median is pivotal in maintaining the triangle’s symmetry and aesthetic appeal. By focusing on the median divisor, we can uncover inherent patterns that may lead to the discovery of new perfect numbers or provide insights into prime structures beyond the Euclid-Euler framework.

2. Examples

a) Example 1: Perfect Number 6

• Triangular Number: \( T_3 = 6 \)
• Divisors: 1, 2, 3, 6
• Total Number of Divisors: 4
• Median Divisor: 2

For the triangular number 6, its divisors are \( \{1, 2, 3, 6\} \). With a total of 4 divisors, the median divisor is the second divisor in the sorted list, which is 2. This divisor acts as the median of the triangle, ensuring that the arrangement of dots maintains symmetry, reflecting the number’s perfect nature.

In the image below, it is the beautiful triangular number 6, the purple dots illustrate the median with a value of \( 2 \) and a side length of \( 3 \).

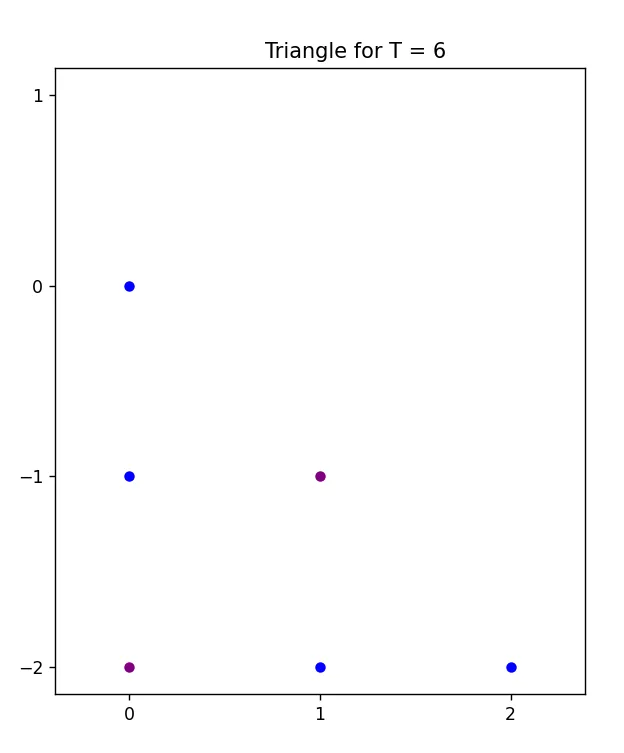
b) Example 2: Perfect Number 28

• Triangular Number: \( T_7 = 28 \)
• Divisors: 1, 2, 4, 7, 14, 28
• Total Number of Divisors: 6
• Median Divisor: 4

Similarly, for the triangular number 28, its divisors are \( \{1, 2, 4, 7, 14, 28\} \). With a total of 6 divisors, the median divisor is the third divisor in the sorted list, which is 4. This central divisor maintains the triangle’s symmetry, reflecting the number’s perfection through its balanced structure.

In the image below, for the beautiful triangular number 28, the purple dots illustrate the median with a value of \( 4 \) and a side length of \( 7 \).

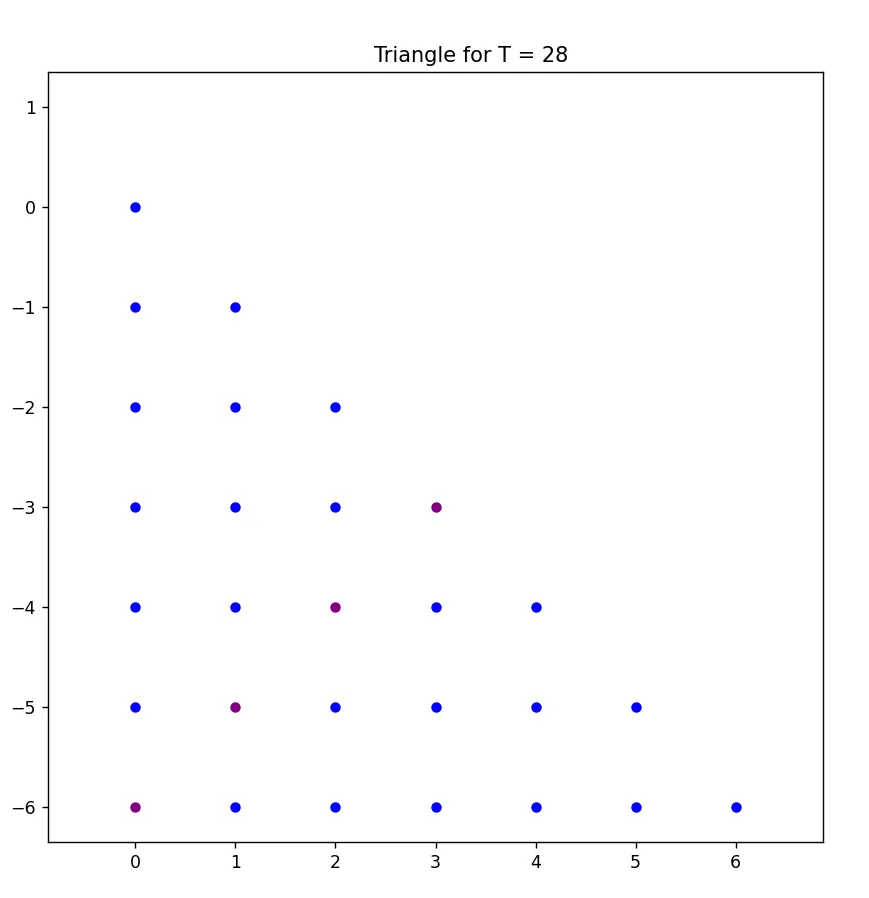
3. Significance of Divisor Arrangement

The strategic arrangement of divisors within a triangular number is not merely a mathematical curiosity; it holds significant implications for the identification and classification of beautiful triangular numbers. By focusing on the median divisor and its role in maintaining symmetry, we can develop algorithms that efficiently detect and analyze beautiful triangular numbers, thereby advancing the search for new perfect numbers and uncovering deeper mathematical relationships.

VI. Sigma Rectangular Numbers: A Subclass within Pronic Number Theory

Building upon the foundational concepts of perfect numbers and beautiful triangular numbers, we introduce a new construct: the Sigma Rectangular Number. This concept leverages Euler’s sigma function to transform the divisors of a triangular number into a mirrored rectangular structure. By doing so, we explore deeper symmetrical relationships within the realm of number theory, potentially unveiling new patterns and insights.

1. Understanding the Sigma Function

The sigma function, denoted as \( \sigma(n) \), is a well-established function in number theory introduced by Euler. It is defined as the sum of all positive divisors of a positive integer \( n \), including \( n \) itself. Formally:

$$ \sigma(n) = \sum_{d \mid n} d $$

For example:

• \( \sigma(6) = 1 + 2 + 3 + 6 = 12 \)
• \( \sigma(28) = 1 + 2 + 4 + 7 + 14 + 28 = 56 \)

In the context of perfect numbers, a number \( n \) is perfect if \( \sigma(n) = 2n \). This property underscores the intrinsic balance within perfect numbers, where the sum of their divisors equals twice the number itself.

2. Defining Sigma Rectangular Numbers

A Sigma Rectangular Number is derived by applying the sigma function to a beautiful triangular number and organizing the resulting sum into a mirrored rectangular structure. This process reveals symmetrical patterns and relationships that are not immediately apparent through traditional analysis.

Formally, given a beautiful triangular number \( T_k \), the Sigma Rectangular Number \( R_k \) is defined as:

$$ R_k = \sigma(T_k) $$

Where \( \sigma(T_k) \) is the sum of all divisors of the triangular number \( T_k \). The resulting number \( R_k \) can then be visualized as a rectangle, where the arrangement of its factors mirrors the structural properties of \( T_k \).

3. Illustrative Examples

To elucidate the concept of Sigma Rectangular Numbers, we examine two prominent perfect numbers: 28 and 496.

a) Example 1: Perfect Number 28

• Triangular Number: \( T_7 = 28 \)
• Divisors of 28: 1, 2, 4, 7, 14, 28
• Sum of Divisors (\( \sigma(28) \)): \( 1 + 2 + 4 + 7 + 14 + 28 = 56 \)

Thus, the Sigma Rectangular Number corresponding to 28 is:

$$ R_7 = \sigma(28) = 56 $$

To visualize this, we can arrange the divisors of 28 into a mirrored rectangle:

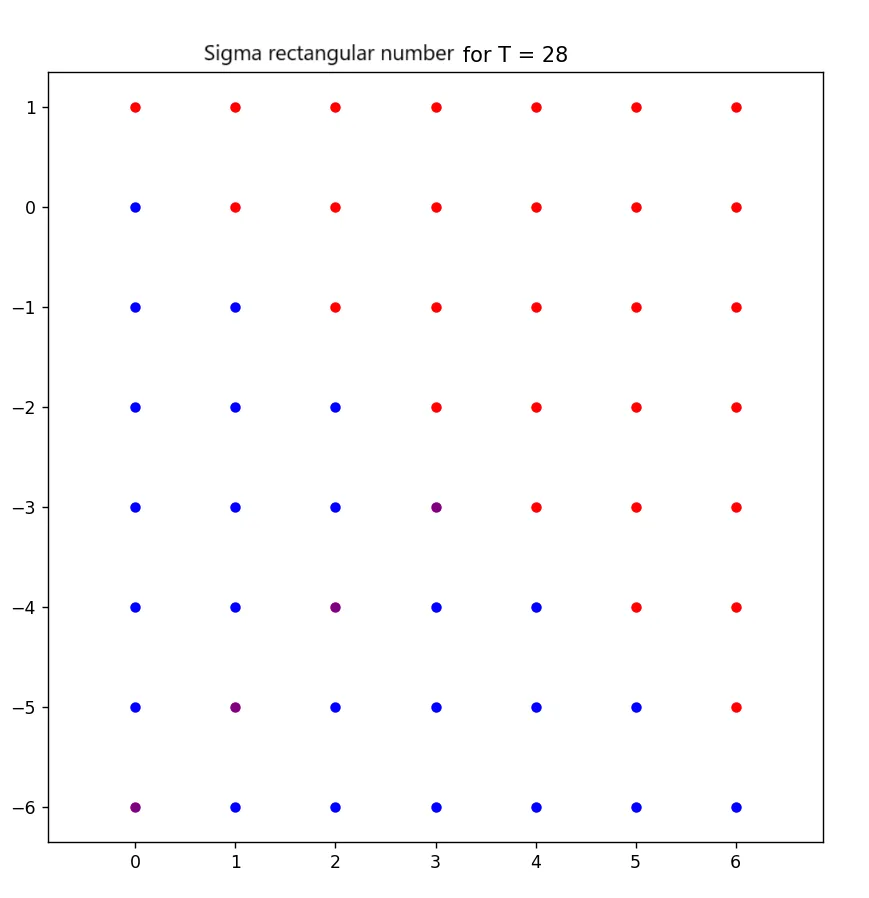
Divisor Pairing:

• \( (1, 28) \)
• \( (2, 14) \)
• \( (4, 7) \)

Each pair multiplies to 28, maintaining symmetry. When arranged in a rectangular format, these pairs form a balanced and mirrored structure, exemplifying the beauty of the Sigma Rectangular Number.

Example 2: Perfect Number 496

• Triangular Number: \( T_{31} = 496 \)
• Divisors of 496: 1, 2, 4, 8, 16, 31, 62, 124, 248, 496
• Sum of Divisors (\( \sigma(496) \)): \( 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 + 496 = 992 \)

Thus, the Sigma Rectangular Number corresponding to 496 is:

$$ R_{31} = \sigma(496) = 992 $$

Visualizing the divisors of 496 as a mirrored rectangle:

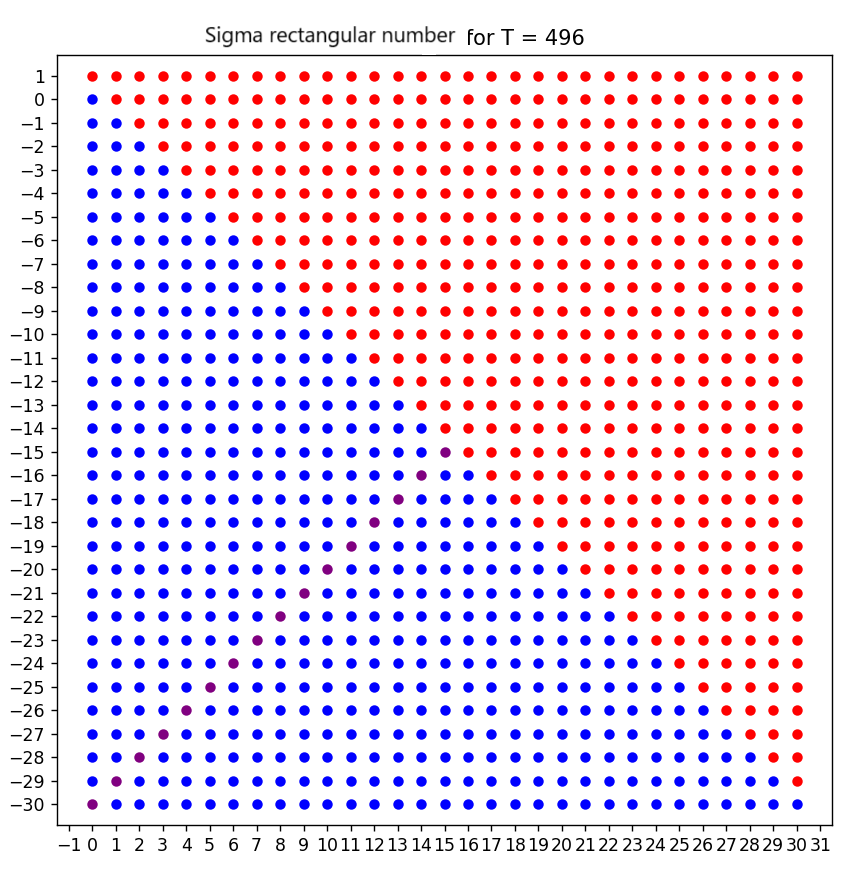
Divisor Pairing:

• \( (1, 496) \)
• \( (2, 248) \)
• \( (4, 124) \)
• \( (8, 62) \)
• \( (16, 31) \)

Each pair multiplies to 496, maintaining symmetry. The arrangement of these pairs into a rectangular structure exemplifies the balanced and mirrored nature of the Sigma Rectangular Number, reflecting the inherent beauty within the number’s divisor relationships.

4. Significance of Sigma Rectangular Numbers

The introduction of Sigma Rectangular Numbers provides a novel lens through which to examine the properties of perfect numbers and their divisors. By focusing on the sum of divisors and their symmetrical arrangement, we uncover deeper insights into the structural balance that defines perfect numbers. This approach not only reinforces the connections established by the Euclid-Euler theorem but also paves the way for exploring new relationships and patterns within number theory.

Furthermore, Sigma Rectangular Numbers offer an alternative pathway to identifying and classifying perfect numbers, potentially extending beyond the traditional reliance on Mersenne primes. By analyzing the divisor structure and their sums, mathematicians can develop algorithms and methodologies that enhance the search for both known and elusive perfect numbers, including the enigmatic odd perfect numbers.

VII. Even Divisors: A Pre-Requirement for Symmetry in Perfect Numbers

The concept of symmetry in divisors is central to understanding even perfect numbers in the Euclid-Euler thoerem. This symmetry, emphasized in Sigma Rectangular Numbers, hinges on the distribution of odd and even divisors. The structure of even perfect numbers inherently restricts odd divisors to:

• 1: The trivial divisor.
• 2^p – 1: The Mersenne prime.

All other divisors of the perfect number are even. This restriction is not coincidental; it is a necessary pre-requirement for the symmetric property of perfect numbers. By ensuring that all divisors except 1 and the Mersenne prime are divisible by 2, the structure of the number is simplified, and the balance in divisor pairs is preserved.

1. Divisors of N

The divisors of N are of the form:

$d\; =\; 2k\times \; m$

where:

• 0 ≤ k ≤ p-1,
• m ∈ {1, 2p - 1}.

a) Odd Divisors:

1. For k = 0, d = m, and m can only be:
   • 1, or
   • 2p - 1 (the Mersenne prime).
2. For k > 0, d = 2k × m becomes even because 2k is divisible by 2.

Thus, the only odd divisors of N are 1 and 2p - 1.

2. Symmetry as a Pre-Requirement

This limitation ensures that the symmetry of divisors emerges naturally. By restricting odd divisors to 1 and the Mersenne prime, the remaining even divisors pair uniquely with each other to form a balanced structure. Any additional odd divisor would disrupt this symmetry, making the number fail to satisfy the perfect number condition. This property aligns with the broader significance of Sigma Rectangular Numbers in uncovering the intrinsic balance within perfect numbers.

For an odd perfect number, however, this principle implies a critical requirement: all divisors must themselves be odd. The structure of odd perfect numbers is conjectured to include constraints such as having multiple distinct prime factors and a unique arrangement ensuring balance and symmetry while remaining entirely odd.

VIII. Rearrangement of Divisors in Sigma Rectangular Numbers

To further explore the concept of Sigma Rectangular Numbers, it is essential to understand how the divisors of a beautiful triangular number are arranged within a rectangular structure. This rearrangement not only highlights the symmetry inherent in perfect numbers but also facilitates the identification of beautiful triangular numbers through their divisor properties.

1. Rearranging Divisors into a Rectangle

The process of rearranging divisors involves organizing them in a specific order to form a mirrored rectangular pattern. The steps are as follows:

1. Sorting Divisors: Begin by listing all the divisors of the beautiful triangular number \( T_k \) in descending order.
2. Pairing Divisors: Pair the largest divisor with the smallest, the second largest with the second smallest, and so on, until reaching the median divisor.
3. Forming the Rectangle: Arrange these pairs into a rectangular structure, where each row contains a pair of divisors that multiply to the triangular number.

This method ensures that the rectangle maintains symmetry, reflecting the balanced nature of perfect numbers.

2. Mathematical Representation

Let \( P \) be an even perfect number, and let \( D(P) = \{d_1, d_2, \ldots, d_n\} \) be its set of divisors sorted in descending order such that:

$$ d_1 > d_2 > \ldots > d_n $$

To rearrange these divisors into a Sigma Rectangular Number, we define a pairing function \( R \) that pairs each divisor with its corresponding counterpart:

$$ R(i) = (d_i, d_{n – i + 1}) \quad \text{for} \quad i = 1, 2, \ldots, \frac{n}{2} $$

Here, \( R(i) \) represents the \( i \)-th row in the rectangular arrangement, where the first element is the \( i \)-th largest divisor and the second element is the \( i \)-th smallest divisor.

Thus, the Sigma Rectangular Number \( \mathcal{R}(P) \) can be visualized as:

$$ \mathcal{R}(P) = \begin{pmatrix} R(1) \\ R(2) \\ \vdots \\ R\left(\frac{n}{2}\right) \end{pmatrix} $$

3. Illustrative Examples

To elucidate this rearrangement process, we examine two prominent perfect numbers: 28 and 496.

a) Example 1: Perfect Number 28

• Triangular Number: \( T_7 = 28 \)
• Divisors: 1, 2, 4, 7, 14, 28
• Total Number of Divisors: 6

Following the rearrangement steps:

1. Sorting Divisors: \( D(28) = \{28, 14, 7, 4, 2, 1\} \)
2. Pairing Divisors:
   • Pair 1: \( (28, 1) \)
   • Pair 2: \( (14, 2) \)
   • Pair 3: \( (7, 4) \)
3. Forming the Rectangle:

The Sigma Rectangular Number \( \mathcal{R}(28) \) is:

$$ \mathcal{R}(28) = \begin{pmatrix} (28, 1) \\ (14, 2) \\ (7, 4) \end{pmatrix} $$

This arrangement showcases a balanced and symmetrical structure, where each row’s product equals the perfect number 28.

The Pattern:

We begin by identifying all divisors prior to confirming the prime structure:

• First largest divisor: 14 dots

Once the prime is identified, its paired divisor represents the median divisor:

• Second largest divisor: 7 dots (Mersenne Prime)
• Median divisor: 4 dots

The remaining divisors align in the final column:

• First least divisor: 2 dots
• Unit divisor: 1 dot

Note: In the illustration below, the first section extends across the median, so the dots corresponding to the median divisor are not included in the count.

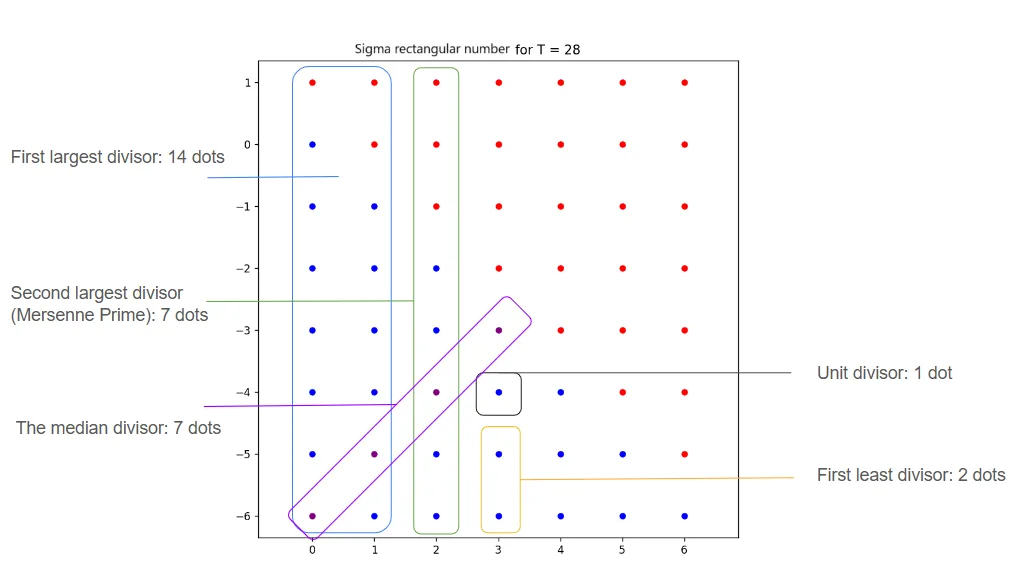
b) Example 2: Perfect Number 496

• Triangular Number: \( T_{31} = 496 \)
• Divisors: 1, 2, 4, 8, 16, 31, 62, 124, 248, 496
• Total Number of Divisors: 10

Following the rearrangement steps:

1. Sorting Divisors: \( D(496) = \{496, 248, 124, 62, 31, 16, 8, 4, 2, 1\} \)
2. Pairing Divisors:
   • Pair 1: \( (496, 1) \)
   • Pair 2: \( (248, 2) \)
   • Pair 3: \( (124, 4) \)
   • Pair 4: \( (62, 8) \)
   • Pair 5: \( (31, 16) \)
3. Forming the Rectangle:

The Sigma Rectangular Number \( \mathcal{R}(496) \) is:

$$ \mathcal{R}(496) = \begin{pmatrix} (496, 1) \\ (248, 2) \\ (124, 4) \\ (62, 8) \\ (31, 16) \end{pmatrix} $$

This mirrored arrangement maintains the symmetry, where each row’s product equals the perfect number 496, highlighting the balanced nature of its divisors.

Applying the Divisor Pattern:

We start by identifying the largest divisors in descending order:

• First largest divisor: 248 dots
• Second largest divisor: 124 dots
• Third largest divisor: 62 dots

The next divisor, paired with the prime, defines the median divisor:

• 4th largest divisor: 31 dots (Mersenne Prime)
• Median divisor: 16 dots

The remaining divisors proceed in ascending order:

• Third least divisor: 8 dots
• Second least divisor: 4 dots
• First least divisor: 2 dots
• Unit divisor: 1 dot

Note: In the illustration below, the first section still extends across the median, so, again the dots corresponding to the median divisor are not included in the count.

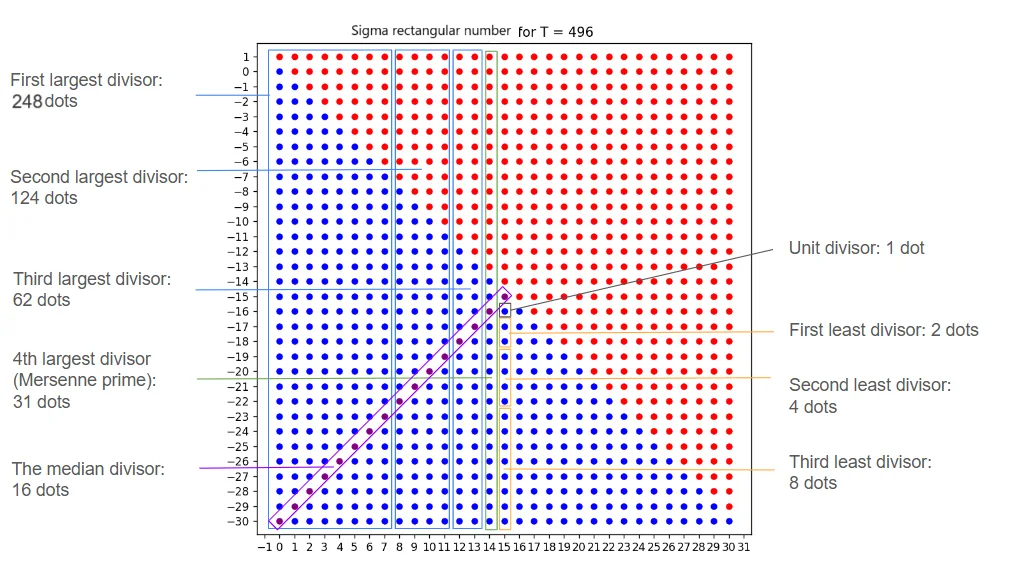
4. Mathematical Formula Describing the Rearrangement

The rearrangement of divisors into a Sigma Rectangular Number can be mathematically described using the following formula:

$$ \mathcal{R}(P) = \begin{pmatrix} (d_1, d_n) \\ (d_2, d_{n-1}) \\ \vdots \\ \left(d_{\frac{n}{2}}, d_{\frac{n}{2} + 1}\right) \end{pmatrix} $$

Where:

• \( P \): An even perfect number.
• \( D(P) = \{d_1, d_2, \ldots, d_n\} \): The set of divisors of \( P \), sorted in descending order.
• \( n \): The total number of divisors of \( P \).

This formula pairs each divisor \( d_i \) with its corresponding counterpart \( d_{n – i + 1} \), ensuring that each pair multiplies to the perfect number \( P \). The arrangement continues until all pairs up to the median divisor are formed, resulting in a symmetrical and balanced rectangular structure.

5. Significance of the Rearrangement

The Sigma Rectangular Number’s rearrangement emphasizes the inherent symmetry within perfect numbers. By pairing the largest divisors with the smallest, and proceeding inward towards the median divisor, we uncover a balanced structure that mirrors the number’s perfection. This symmetrical arrangement not only provides aesthetic appeal but also offers a structured method to analyze and identify perfect numbers through their divisor properties.

Moreover, this rearrangement facilitates the development of algorithms aimed at detecting beautiful triangular numbers. By systematically organizing divisors into a mirrored rectangle, patterns and relationships emerge that can be leveraged to explore perfect numbers beyond the traditional Euclid-Euler framework, potentially paving the way for the discovery of new perfect numbers or insights into the elusive odd perfect numbers.

IX. Creating the Algorithm for Identifying Beautiful Triangular Numbers

To systematically identify beautiful triangular numbers, we develop an algorithm that analyzes the divisors of a triangular number and verifies specific structural properties. This algorithm leverages mathematical functions and logical checks to determine whether a given triangular number qualifies as beautiful based on the defined criteria.

1. Algorithm Overview

The algorithm follows a series of steps to validate a triangular number \( T \) as beautiful. Below is a detailed breakdown of each step, accompanied by the relevant mathematical formulas:

1. Triangularity Verification: Confirm that the number \( T \) is a triangular number by solving for \( n \) in the triangular number formula.
2. Median Length Calculation: Determine the median length of the triangle based on \( T \) and \( n \).
3. Sigma Rectangular Number Computation: Calculate the Sigma Rectangular Number \( R \) using Euler’s sigma function.
4. Divisor Pairing and Section Validation: Arrange the divisors of \( T \) into paired sections within the rectangular structure and validate each section.
5. Final Validation: Ensure that all divisors are correctly paired and that the median properties hold.

2. Step-by-Step Algorithm Explanation

a) Triangularity Verification

Given a number \( T \), first verify that it is a triangular number by solving for \( n \) in the equation:

$$ n = \frac{-1 + \sqrt{1 + 8T}}{2} $$

If \( n \) is an integer, \( T \) is a valid triangular number. This is derived from the inverse of the triangular number formula:

$$ T = \frac{n(n + 1)}{2} $$

b) Median Length Calculation

Once \( T \) is confirmed as a triangular number, calculate the median length (\( \text{median_length} \)) of the triangle:

$$ \text{median_length} = \frac{T}{n} $$

This represents the number of dots along the median of the triangular arrangement.

c) Sigma Rectangular Number Computation

Compute the Sigma Rectangular Number (\( R \)) using Euler’s sigma function, which sums all positive divisors of \( T \):

$$ R = \sigma(T) = 2T $$

For perfect numbers, this relationship holds true because the sum of their divisors equals twice the number itself.

d) Divisor Pairing and Section Validation

Arrange the divisors of \( T \) into a mirrored rectangular structure by following these steps:

1. Identify Divisors: List all divisors of \( T \) in descending order.
2. Pair Divisors: Pair the largest divisor with the smallest, the second largest with the second smallest, and so on, until reaching the median divisor.
3. Calculate Columns and Rows: Determine the number of columns in each section by dividing the median length by the first divisor. The number of rows in the rectangle is \( n + 1 \), where the \( +1 \) accounts for the shifted mirrored triangle configuration previously discussed.
4. Validate Sections: For each paired divisor, calculate the number of dots in the section (rows multiplied by columns) and verify that it matches the corresponding divisor.

Mathematically, for each divisor pair \( (d_i, d_{n-i+1}) \), the following must hold:

$$ \text{Dots in Section} = \text{Rows} \times \text{Columns} = d_i $$

e) Final Validation

After arranging and validating all sections, ensure that:

• The sum of the divisors after the median equals \( \text{median_length} – 1 \).
• The remaining dots correspond to the median divisor.

If all validations pass, \( T \) is confirmed as a beautiful triangular number.

3. Mathematical Formula Describing the Algorithm

The algorithm can be encapsulated in the following mathematical framework:

1. Determine Triangularity:

   Given a number \( T \), compute:

   $$ n = \frac{-1 + \sqrt{1 + 8T}}{2} $$

   If \( n \) is an integer, proceed to the next steps.

2. Calculate Median Length:

   Compute:

   $$ \text{median_length} = \frac{T}{n} $$

3. Compute Sigma Rectangular Number:

   For a perfect number, calculate:

   $$ R = \sigma(T) = 2T $$

4. Pair Divisors:

   List the divisors \( D(T) = \{d_1, d_2, \ldots, d_n\} \) in descending order. Pair them as:

   $$ R(i) = (d_i, d_{n-i+1}) \quad \text{for} \quad i = 1, 2, \ldots, \frac{n}{2} $$

   Arrange these pairs into a rectangular structure.

5. Validate Sections:

   For each pair \( R(i) \), ensure:

   • Columns in Section \( i \): \( \frac{\text{median_length} – \sum_{j=1}^{i-1} \text{columns}_j}{\text{first divisor of Section } i} \)
   • Dots in Section \( i \): \( \text{rows} \times \text{columns} \)
   • Verification: \( \text{Dots in Section } i = d_i \)
6. Final Check:

   Confirm that the sum of divisors after the median equals the median length minus one, and that the remaining dots align with the median divisor.

This formulaic approach ensures that each step of the algorithm maintains mathematical integrity, validating the beautiful triangular nature of the number \( T \).

a) Example 1: Perfect Number 496

1. Triangularity Verification:
   • Compute \( n = \frac{-1 + \sqrt{1 + 8 \times 496}}{2} = \frac{-1 + \sqrt{3969}}{2} = \frac{-1 + 63}{2} = 31 \).
   • Since \( n = 31 \) is an integer, \( T = 496 \) is a valid triangular number.
2. Median Length Calculation:
   • \( \text{median_length} = \frac{496}{31} = 16 \).
3. Sigma Rectangular Number Computation:
   • \( R = \sigma(496) = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 + 496 = 992 \).
4. Divisor Pairing and Section Validation:
   • Divisors of 496: \( \{496, 248, 124, 62, 31, 16, 8, 4, 2, 1\} \).
   • Pairing:
     • Pair 1: \( (496, 1) \).
     • Pair 2: \( (248, 2) \).
     • Pair 3: \( (124, 4) \).
     • Pair 4: \( (62, 8) \).
     • Pair 5: \( (31, 16) \).
   • Columns in First Section: \( \frac{16}{2} = 8 \).
   • Rows of the Rectangle: \( 31 \).
   • Dots in First Section: \( 31 \times 8 = 248 \).
   • Validation: \( 248 \) matches the first divisor pair \( (248, 2) \) since \( 248 \times 2 = 496 \).
   • Creating Next Sections:
     • Pair 2: \( (124, 4) \). Columns: \( \frac{16 – 8}{2} = 4 \).
     • Dots: \( 31 \times 4 = 124 \). Validation: \( 124 \) matches \( 124 \times 4 = 496 \).
     • Pair 3: \( (62, 8) \). Columns: \( \frac{16 – 8 – 4}{2} = 2 \).
     • Dots: \( 31 \times 2 = 62 \). Validation: \( 62 \) matches \( 62 \times 8 = 496 \).
     • Pair 4: \( (31, 16) \). Columns: \( \frac{16 – 8 – 4 – 2}{2} = 1 \).
     • Dots: \( 31 \times 1 = 31 \). Validation: \( 31 \) matches \( 31 \times 16 = 496 \).
5. Final Validation:
   • Sum of divisors after median: \( 15 \).
   • Remaining dots on the last column: \( \frac{31}{2} – 1 = 15 \) (since \( 31 \) is odd, we round down to 15).
   • Sum \( 15 = 8 + 4 + 2 + 1 \) (including the unit divisor).
   • Validation passes, confirming \( T = 496 \) as a beautiful triangular number.

Since all validations are successful, \( T = 496 \) is confirmed as a beautiful triangular number.

4. The Exception

In the study of beautiful triangular numbers, an interesting exception arises with the number 6.

a) Why 6 Does Not Fit the Pattern

1. Unique Mathematical Properties

• Perfect Number: 6 is the smallest perfect number, meaning it is equal to the sum of its proper divisors:
  $$6 = 1 + 2 + 3$$
• Semiprime: It is also the only perfect number that can be expressed as the product of two prime numbers:
  $$6 = 2 \times 3$$

2. Breakdown of the Pattern

• Side Length Multiplied Directly by Median Divisor: In the case of 6, the side length \( n = 3 \) multiplied directly by the median divisor results in the triangular number itself, bypassing the need for sections that are critical in the pattern for larger beautiful triangular numbers.
• Lack of Remaining Divisors for Subsequent Sections: After accounting for the first section in the algorithm, there are no remaining divisors that appropriately fit into the subsequent columns or sections. This discrepancy arises because the small size and unique properties of 6 cause the standard pattern to break down.

3. Illustration of the Issue

First Section:

• Columns: The median length divided by the first divisor (which is 2 for even triangular numbers) gives columns in the first section:
  $$\text{columns} = \frac{\text{median_length}}{2}$$
• Dots in First Section: $$(\text{rows} – 1) \times \text{columns}$$

Remaining Sections: There are no remaining divisors that correspond to the subsequent sections’ dots, making it impossible to continue the pattern beyond the first section.

b) Conclusion on 6’s Exceptionality

The number 6 does not satisfy the criteria for beautiful triangular numbers, as the required pattern of sections and divisors cannot extend beyond the initial calculation. Its exclusion in algorithmic results is due to its unique properties: as a semiprime triangular number, it takes the form:

$$ T = \text{side} \times \text{median} $$

with no remaining divisors for subsequent sections. This structure arises from 6 being the product of two primes, limiting the partitioning required for larger beautiful triangular numbers.

4. Conclusion

The creation of this algorithm offers a systematic method for identifying beautiful triangular numbers by meticulously analyzing their divisors and validating their structural properties. By leveraging mathematical functions such as the sigma function and applying logical checks for symmetry and balance, the algorithm not only reinforces the established relationships between perfect numbers and triangular numbers but also paves the way for discovering new patterns and potential perfect numbers beyond the traditional Euclid-Euler framework.

This innovative approach exemplifies the synergy between mathematical theory and computational techniques, highlighting the potential for algorithmic advancements to uncover deeper insights within number theory.

For more details, refer to the code implementation.

X. Hypothesis on the Non-Existence of Odd Perfect Numbers

This work proposes a structural hypothesis suggesting that odd perfect numbers cannot exist, based on specific patterns identified within a new algorithmic framework. The symmetry required for a number to be perfect, where the sum of its divisors equals the number itself, relies on a particular structural configuration that is inherently unattainable in odd numbers.

As we saw previously, an odd perfect number would require all its divisors to be odd, which means they must share a specific prime-divisibility structure. For example, the divisors could potentially involve a power of \(3\) as a least prime. However, having at least one such least prime is necessary to maintain the required balance and symmetry among the divisors. This ensures that all divisors, except \(1\) and the number itself, remain odd and form a coherent structure under the perfect number condition.

This requirement is essential to maintaining the necessary symmetry among divisors, as demonstrated by the algorithm. However, for a power of 3 to satisfy the conditions for perfection, it would need to be also divisible by both 5 and 7. Since no power of 3 can include 5 and 7 as factors (powers of 3 only contain 3 as a prime factor), it is impossible for an odd number to satisfy the structural requirements needed for perfection.

For a number to be perfect, the sum of its proper divisors must equal the number itself. This requires a balanced structure of divisors, where smaller divisors pair with larger ones to symmetrically add up to the number. If we consider a power of 3, such as 3k, satisfying the conditions for perfection would demand the following:

1. Contribution of Divisors

• A power of 3 has divisors only of the form 1, 3, 32, ..., 3k-1. Without additional primes like 5 and 7, the divisor sum is constrained by this limited set, making it almost impossible for their sum to reach 3k.
• Adding other small primes like 5 and 7 introduces more divisors, effectively increasing the divisor sum and balancing the contributions from small and large divisors.

2. Symmetry and Pairing

• Perfect numbers rely on the pairing of divisors, where smaller divisors pair with larger ones. As the least prime divisor becomes larger (e.g., starting only with 3 rather than including 5 or 7), the corresponding largest divisors shrink.
• This reduction in the size of the largest divisors diminishes their contribution to the divisor sum, making it less likely for the sum to reach the number itself.

3. Probability of Reaching Perfection

• As the smallest prime divisor increases, the structure becomes less flexible, and the range of small potential divisors narrows.
• Without additional small primes like 5 and 7, the largest divisors of the number will be insufficient to compensate for the sum of the smaller ones, significantly reducing the probability of the number being perfect.

Why 5 and 7 Are Needed

Including additional primes like 5 and 7 ensures a richer set of divisors, allowing for larger paired divisors that can effectively balance the sum. Without this, a power of 3 alone would fail to meet the perfection criterion because the divisor sum would fall short. Thus, divisors divisible by 5 and 7 are necessary to expand the structure and increase the chances of reaching the required total.

This observation is further supported by examining odd abundant numbers, such as 945, 1575, 2205, 2835, and 3465. Each of these numbers has factors such as 3, 5, and 7, which contribute to their abundance but also disrupt the necessary power-of-3 structure, creating an asymmetry that prevents these numbers from summing precisely to themselves. In other words, the presence of additional primes, like 5 and 7, breaks the divisor pairing required for a perfect sum.

Therefore, based on the need for a power-of-3 structure and the impossibility of satisfying this structure with factors of 5 and 7, we conclude that odd perfect numbers cannot exist within this framework. This hypothesis is consistent with all known results in perfect numbers and supports the conjecture that odd perfect numbers are unlikely. To prove this, one must demonstrate that no median divisor can be a power of 3 while its paired divisor is an odd prime, and that all larger divisors up to the prime are divisible by 3.